十八：包围盒（上）

我们开开心心的讲完了中篇的前两章，渲染出了炫酷的动态模糊效果，它简单而且漂亮。但是，该来的总归还是要来，下面的几章会给大伙儿整些头疼的：包围盒。

光线碰撞中的重复冗余

回顾一下我们发射光线到回收颜色的全过程，就会发现，我们的代码有哪些不合理的地方：

相机朝虚拟视口中的像素格子发出光线，这跟光线会尝试调用场景中所有物体（本项目中一个名为world的物体列表）的hit函数——会按物体插入物体列表时候的顺序对物体进行逐一调用它们自己的hit函数。这些子物体要不还是物体列表，或者是球、移动的球之类的实体物体。

我们再来看看球和移动的球是如何处理光线碰撞的，我们通过解一个二元一次方程来判断球是否和光线碰撞，返回碰撞时刻以及碰撞点信息等等（具体见《球》）。这意味着对于每一次射出光线（无论是相机射出的，还是材质表面反射得来的）都要和场景中所有的球进行一次判断。如果场景中有100个物体，意味着，每一次hit之后反射的光线，就要解100个二元一次方程。假设平均每根光线会在场景中弹射5次，对于每一根光线我们要解500个方程，采样数会把这个数字拉到50000（假设每个像素采样100次），而像素数量会把这个数字拉到亿级别（假设我们的场景是400*300），现在看看我们球类代码中的hit函数，那么一大坨，你能想象每次在命令行中点击回车，电脑运行了几亿次这部分的代码吗？

不合理的地方在哪里呢？假设我们有一个光线朝西边径直而去，在光线射过去的方向的相反方向有99颗球，这九十九颗球也都逃不过碰撞检测函数。这分莫名其妙的开销应该是可以通过某种方式避免的。

总结一下刚刚所说的：光线-物体交集是光线追踪器中的主要时间瓶颈，时间与物体数量成线性关系。这是对同一模型的重复冗余搜索，有没有什么办法可以使之复杂度降低呢？比如通过某种二分法让其的复杂度降低到对数等级？

空间划分与八叉树

我提到了二分法，但应该知道，二分法必须针对已排序的数据才有作用，也就是说，我们必须让场景中的物体依照某种规则变得有序，才可以使用二分法的思想降低复杂度。

假设我们的物体都集中在以原点为中心的单位立方体里面，很容易可以想到一种划分方式：先通过三个坐标轴把空间划分为八个小立方体。

如果把任意一个数带入t，光线的公式，最终得到的坐标点的x,y,z都不会大于0，那我们就没有必要检查位于第Ⅰ象限的物体了。如果x,y,z有全大于0的情况，说明光线与第Ⅰ象限有交点，我们就对第一象限中的小立方体继续划分——划分成八个更小的立方体，再检查光线是否与它们有交点，位于和光线无交点的小立方体内的物体，我们就无需检查了。这种思想叫空间划分。

整个搜索链条就如同树一样，先看有没有和大立方体有交集，如果有交集就再看其中的小立方体，然后一直往下看，直到我们人为规定的某个大小的立方体内不再有更小的立方体，就直接查看该立方体内的物体即可。

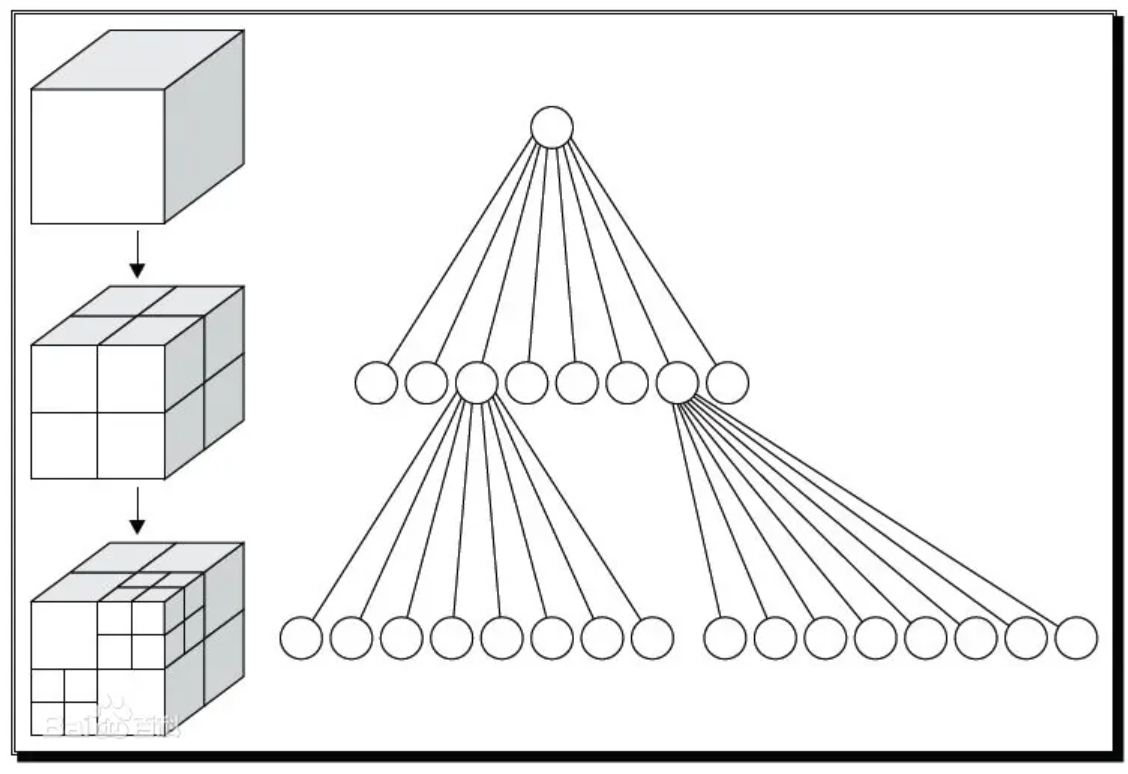
八叉树——这种结构有一个浅显易懂的名字。很容易可以写出关于八叉树的伪代码（这个八叉树只有两层，第三层就是物体层）：

if (光线碰到了某个立方体)
    if(光线碰到了子立方体1号){
        if(光线碰到了子立方体1号内的某个物体){
            处理碰撞信息。
            return true;
        }
    }
    else if(光线碰到了子立方体2号){
        ...
    }
    ...
    else if(光线碰到了子立方体7号){
        ...
    }
    else{
        ...
    }
else
    return false

我们没有讨论如何判断光线和立方体求交，也没有讨论物体在两个立方体的边界上我们要如何处理，篇幅有限。我们不会在项目中使用八叉树，但是它确实是一个可行的方案，并且很容易被图形工程师们提起。

我们并不准备使用空间划分的八叉树来管理我们场景中的物体，因为还有另一个备选方案可以使用——对象划分。这种空间划分比空间划分使用更为广泛。

对象划分简述

现在假设空间中有15个对象，我们按照某种规律把它们分成俩个部分，如下图所示：

至于划分对象的算法我们之后再说。

这是三维空间的某种对象划分在二维上的投影示意图。可见对象划分之后的各个区域是很可能会重叠的，但是也就不再存在一个物体处于区域边界的情况。

当然这里也依然存在一个树状结构。光线先和最外层和紫色部分算交点，如果存在交点才会查看红蓝两个区域的交点情况。

AABB

我们已经决定使用对象划分来加速光线碰撞，这里有很多问题待解决：具体如何划分物体？树状结构如何搭建？新的场景物体又该如何管理（物体列表显然已经不满足要求了）？

这些问题先靠一边，我们先来把目光瞄准到所谓“区域”，也就是包围盒。

包围盒应该是什么样的？我们又如何计算光线与盒子求交呢？

如果不考虑性能，包围盒可以是任何形状，它可以是一个大球，包裹住内部的小球，这样我们只需要算一次一元二次方程就可以得到光线和大球碰撞的结果，如果有碰撞再计算光线和内部小球的碰撞情况。而且我们计算光线和大球求交的时候不需要计算具体反射光线，完全不需要调用材质代码，只需要返回是否碰撞到信息，以便我们去判断需不需要和内部小球进一步计算碰撞即可。

但是光线和球的碰撞计算复杂度还是高了一点，有一种结构最擅长处理和光线求交，这就是轴向立方体。使用轴向立方体作为包围盒的形状，这就是轴向包围盒（**Axis-Aligned Bounding Boxes ），又叫AABB**。

轴向立方体就是所有的边都和坐标轴平行的立方体，它和光线求交的计算复杂度低，且易于理解。

先不看Z轴，在平面上的轴向包围盒如下图所示，空间中的包围盒和其原理相同，可以通过推广得到：

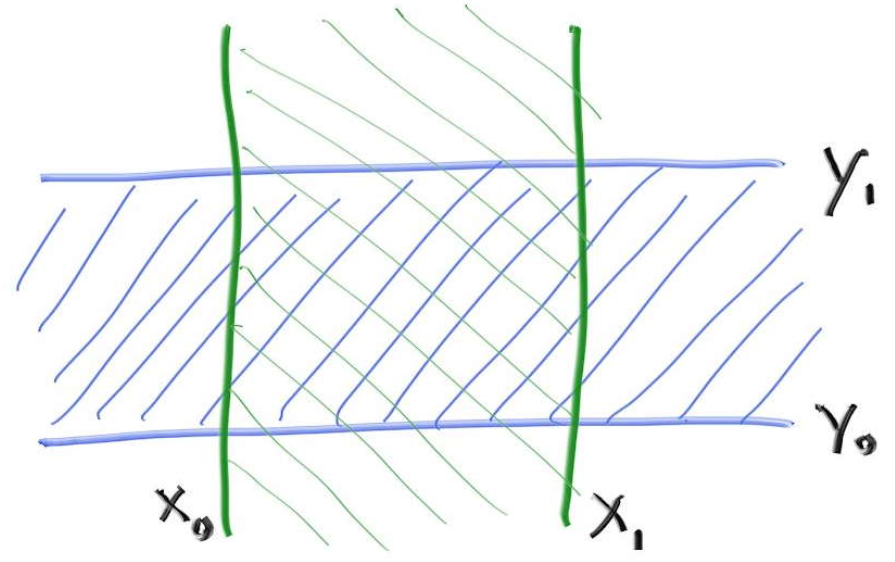
平面上的AABB（2D-AABB）即是四条直线围成的区域。对于这对平行线，光线会和它们产生两个交点，当然，另外一对平行线同理：

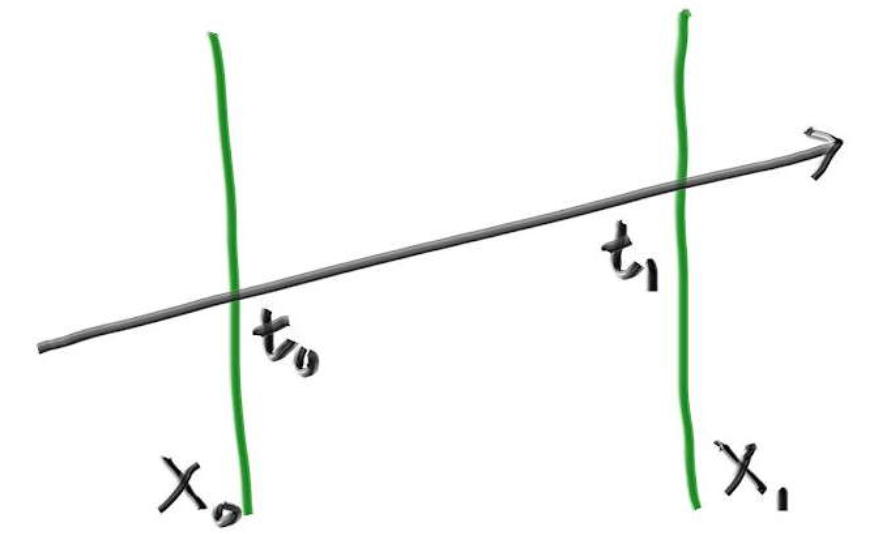
看看光线传播到$x$分量为和$x_0$时$x_1$，时间$t_1$和$t0$是多少，只要把光线原点位置坐标向量A的x分量和方向向量b的x分量带入公式$P(t) = A + tb$即可：

和

同理，在y轴上你同样可以得到两个时间：

和

好，有了这四个时间值，我们如何判断这根光线有没有和2D-AABB相交呢？看下图：

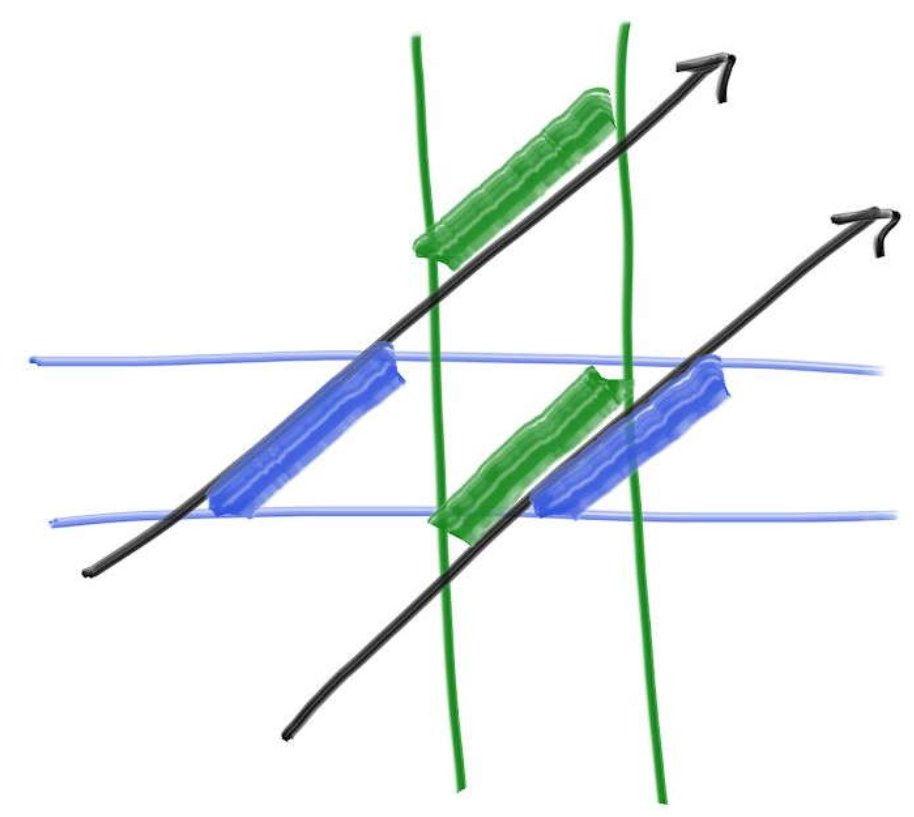
对于上图中上方的光线，其(t0,t1)和(t2,t3)两个时间区域并无交集，在图中的表现即是蓝色和绿色的线段并无重合处，那就可以断言，这根光线和盒子并无交集。而下面的光线可见明显蓝绿重合，它一定是一根穿过盒子的光线。

很容易就能把这个原理推广到三维的情形下：

3D-AABB由三对面组成，假设光线传播到与XoY面平行的那一对面上的时间是t0,t1，传播到YoZ面上的时间t2,t3，ZoX则是t4,t5。则一定有：光线和盒子相交 <==> (t0,t1)、(t2,t3)和(t4,t5)两两有交集。

伪码如下：

compute (tx0, tx1)
compute (ty0, ty1)
compute (tz0, tz1)
//返回这三个时间段有无重叠
return overlap?( (tx0, tx1), (ty0, ty1), (tz0, tz1))

对于坐标轴上的两个区间(a,b)和(c,d)，判断区间有无重叠，只需要取a和c较大的那一个和b与d中较小的那一个比较，如果前者小于后者，说明有重叠，这部分的伪码如下：

bool overlap(a, b, c, d)
    f = max(a, c)
    F = min(b, d)
    return (f < F)

铺垫完成，接下来我们来从代码层面构造AABB。

编写AABB类

创建aabb.h文件，敲入如下代码：

#ifndef AABB_H
#define AABB_H

#include "rtweekend.h"

class aabb {
    public:
        aabb() {}
        // 如何唯一确定一个3D-AABB？只需要两个点即可！
        aabb(const point3& a, const point3& b) { minimum = a; maximum = b;}

        //返回三个分量都较小的那一个点。
        point3 min() const {return minimum; }
        //返回minimum点在盒子上的对角点，即三个分量都较大的那个点。
        point3 max() const {return maximum; }

        //光线和AABB求交代码，注意这个hit和物体类的hit没有一毛钱关系。
        bool hit(const ray& r, double t_min, double t_max) const {
            //for循环判断三个轴向的三对面和光线碰撞的时间。
            for (int a = 0; a < 3; a++) {
                //见解析。
                auto t0 = fmin((minimum[a] - r.origin()[a]) / r.direction()[a],
                               (maximum[a] - r.origin()[a]) / r.direction()[a]);
                auto t1 = fmax((minimum[a] - r.origin()[a]) / r.direction()[a],
                               (maximum[a] - r.origin()[a]) / r.direction()[a]);
                t_min = fmax(t0, t_min);
                t_max = fmin(t1, t_max);
                if (t_max <= t_min)
                    return false;
            }
            return true;
        }
        
    
        point3 minimum;
        point3 maximum;
};

#endif

​ 我们使用两个point3来唯一确定一个3D-AABB，就如同我们可以在平面直角坐标系上用左下角和右上角两个点确定一个2D-AABB一样。

我们来看看hit函数里的for循环中做了什么？

首先，我们把minmum和maximum点的$x$分量都带入了公式$P(t) = A+tb$来计算光线穿过这一对面的时间值$t_0$和$t_1$，注意，这里的fmin和fmax函数是为了确保$t_0$小于$t_1$。因为minmum[0]一定是小于maximum[0]的，但是无法确定$\frac{minimum[0]-A_x}{b_x}$就一定比$\frac{maxmum[0]-A_x}{b_x}$小，想想光线从x轴无穷大处朝x变小的方向射过来，这时候$\frac{minimum[0]-A_x}{b_x}>\frac{maxmum[0]-A_x}{b_x}$，我们就需要调换存储和$t_0$和$t_1$。

紧接着，我们开始对区间求交集。hit函数传进来的t_min和t_max代表我们认可的t的范围，这个与物体类的hit函数的参数中的t_min和t_max是一个道理，用来给我们切去不必要的碰撞（如负值t）的。现在把($t_0$,$t_1$)和(t_min,t_max)求交，得到的值如果是一个不存在的区间，则表示“在您认可的t的区间内，不存在一个t让光线传播到AABB的x轴同向对面中”。

紧接着对y和z轴上的对面做同样的操作，期间一旦发现求交后区间不存在，便可断定“光线在给定的时间区间内不曾跨过指定对面”，对三个对面进行这样的操作之后，求交的结果存在与否则代表了“光线是否在某一时刻同时在三个对面之间，即是否曾射入AABB之中”。

优化hit函数

我们换一种方式描述hit代码中的逻辑，下面的代码比起原先的hit函数冗长的逻辑显得更为清晰。

inline bool aabb::hit(const ray& r, double t_min, double t_max) const {
    for (int a = 0; a < 3; a++) {
        auto invD = 1.0f / r.direction()[a];
        auto t0 = (min()[a] - r.origin()[a]) * invD;
        auto t1 = (max()[a] - r.origin()[a]) * invD;
        //如果光线的方向向量某个分量为负，则光线一定会逆向穿过本轴上的对面。
        if (invD < 0.0f)
            std::swap(t0, t1);
        t_min = t0 > t_min ? t0 : t_min;
        t_max = t1 < t_max ? t1 : t_max;
        if (t_max <= t_min)
            return false;
    }
    return true;
}

给物体绑定包围盒

AABB类已经被构造出来了，我们现在得把它和物体类联系起来了，因为包围盒子终归是要包裹住物体的。

先来修改底层，给物体类添加一个纯虚函数。

#include "aabb.h"
...

class hittable {
    public:
        ...
        virtual bool hit(const ray& r, double t_min, double t_max, hit_record& rec) const = 0;
        //制造包围盒子的函数。
        virtual bool bounding_box(double time0, double time1, aabb& output_box) const = 0;
        ...
};

来看看这个新的函数，首先，它的返回值是bool类型，这是因为我们得给无法被包围盒包裹的物体一个解释，比如一个无限大的平面（以后可能会有），如果返回true，则表示包围盒生成失败。

生成的包围盒通过参数中的引用传递出去 ：aabb& output_box。

至于另外两个参数time0和time1，它对于移动的球类以及后续所有动态的物体都是必要的，因为如果不给定一个时间区间，物体运动的轨迹将会无限长，无法被包围盒包裹。

很容易可以写出球类的包围盒生成函数：

class sphere : public hittable {
    public:
        ...
        virtual bool hit(
            const ray& r, double t_min, double t_max, hit_record& rec) const override;

        //override包围盒生成函数。
        virtual bool bounding_box(double time0, double time1, aabb& output_box) const override;
        ...
};

...
bool sphere::bounding_box(double time0, double time1, aabb& output_box) const {
    //这是一个球的外切立方体。它是能包裹住球且体积最小的AABB。
    output_box = aabb(
        center - vec3(radius, radius, radius),
        center + vec3(radius, radius, radius));
    return true;
}

​ 下面是移动的球类的包围盒生成函数：

...
#include "aabb.h"
...

class moving_sphere : public hittable {
    public:
        ...
        virtual bool hit(
            const ray& r, double t_min, double t_max, hit_record& rec) const override;
        
        //override包围盒生成函数。
        virtual bool bounding_box(
            double _time0, double _time1, aabb& output_box) const override;
        ...
};

...
bool moving_sphere::bounding_box(double _time0, double _time1, aabb& output_box) const {
    //我们先生成移动的球在两个极端时间下的包围盒。
    aabb box0(
        center(_time0) - vec3(radius, radius, radius),
        center(_time0) + vec3(radius, radius, radius));
    aabb box1(
        center(_time1) - vec3(radius, radius, radius),
        center(_time1) + vec3(radius, radius, radius));
    //然后再求这两个包围盒的包围盒。这个surrounding_box函数会在之后给出。
    output_box = surrounding_box(box0, box1);
    return true;
}

​ 下面添加两个包围盒的包围盒函数surrounding_box(box0, box1)到aabb.h中，它的本质是通过比较去筛选包围盒中的两个point3的分量，使得minimum的各个分量取两个盒子的minimum分量的较小值，maximum的所有分量都取两个盒子的maximum分量的较大值，如下所示：

aabb surrounding_box(aabb box0, aabb box1) {
    point3 small(fmin(box0.min().x(), box1.min().x()),
                 fmin(box0.min().y(), box1.min().y()),
                 fmin(box0.min().z(), box1.min().z()));

    point3 big(fmax(box0.max().x(), box1.max().x()),
               fmax(box0.max().y(), box1.max().y()),
               fmax(box0.max().z(), box1.max().z()));

    return aabb(small,big);
}

aabb对于本章开头提到的树状结构来说相当于叶子节点，本章基本完成了叶子节点的构造，但对于整个树状结构的搭建来说，才是刚刚开始。

课后实践

尝试编写物体列表类的包围盒生成函数（这个函数会在下一章给出）。

参考文献

https://raytracing.github.io/books/RayTracingTheNextWeek.html

参考自《Ray Tracing: The Next Week》第3.1节到第3.7节。