斯涅尔定律
折射光线会遵循以下的法则进行折射,这个定律叫折射定律,或者是斯涅尔定律(Snell’s law):
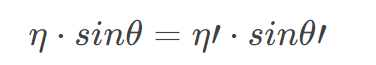
公式中,θ 和 θ′ 是入射光线和折射光线和法线的夹角,η 和 η′ 则是折射率,它表示入射光线所在的介质和折射光线所在的介质的一种性质,是光在真空中的传播速度与光在该介质中的传播速度之比(空气的折射率为1.00029,近似为1,玻璃是1.3-1.7,钻石则是2.4),如下图所示:
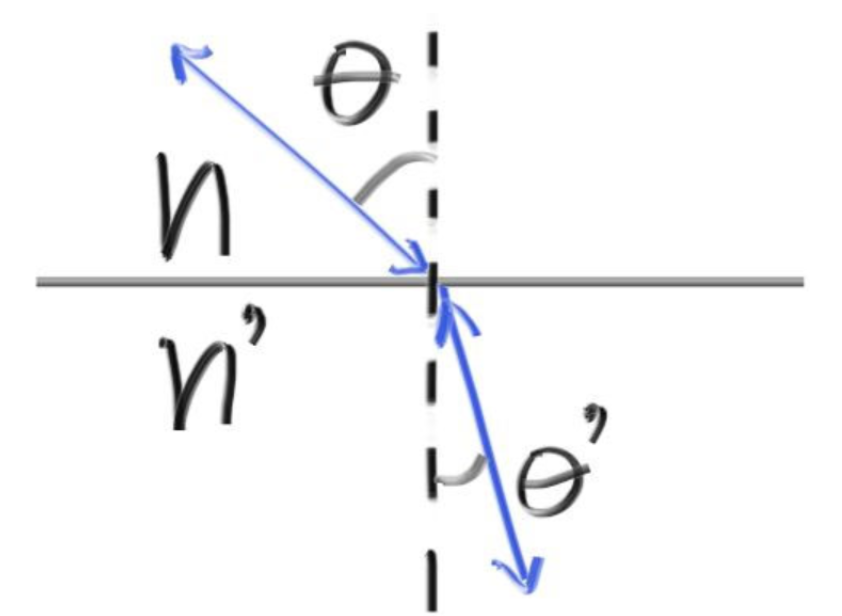
折射方向向量
已知入射向量为R,如何求折射后向量R’呢?直接求是非常困难的,我们对它做一个分解,把目标向量分解到法线和与法线垂直方向这两个互相垂直的方向上,有

先求R’,它是R’中与法线方向垂直的分量。我们清楚的知道它的模是sinθ′ ,但我们得找到一个和法线方向垂直的向量x(上图中指向正右方)作为它的向量表示,即最终的结果就是sinθ′ * unit_vector(x)。
我们可以从入射角那里找到一个这样的向量 x=R+cosθn,它是一个和同$R’⊥向,并且模为sinθ的向量,我们要的向量的模是sinθ′ ,不过没关系,再利用斯涅尔定律转换一下就可以了,解析式如下:

到这一步还不够,我们已知的东西是入射向量和法线向量,θ不应该出现在最终的解析式里。因为R和法线向量n都是单位向量,我们可以用一个点乘去消灭这个碍事的cosθ,即:

知道R’⊥之后,R’∥可以通过一个简单的公式推算得到。首先,是和R’∥和n同向的,它的长度是cosθ′ ,通过三角函数中最基础的公式:

我们就可以得到如下最终解析式:

一切都准备妥当了,在vec3.h中创建一个类外函数,来描述折射这一过程:
1
2
3
4
5
6
7
8
9
|
vec3 refract(const vec3& uv, const vec3& n, double etai_over_etat) {
auto cos_theta = dot(-uv, n);
vec3 r_out_perp = etai_over_etat * (uv + cos_theta*n);
vec3 r_out_parallel = -sqrt(fabs(1.0 - r_out_perp.length_squared())) * n;
return r_out_perp + r_out_parallel;
}
|
总是折射的玻璃
有了折射函数,就先写一个总是折射的透明材质,看代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class dielectric : public material {
public:
dielectric(double index_of_refraction) : ir(index_of_refraction) {}
virtual bool scatter(
const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
) const override {
attenuation = color(1.0, 1.0, 1.0);
double refraction_ratio = rec.front_face ? (1.0/ir) : ir;
vec3 unit_direction = unit_vector(r_in.direction());
vec3 refracted = refract(unit_direction, rec.normal, refraction_ratio);
scattered = ray(rec.p, refracted);
return true;
}
public:
double ir;
};
|
main函数中看一下什么样吧
1
2
3
4
5
6
7
8
| auto material_ground = make_shared<lambertian>(color(0.8, 0.8, 0.0));
auto material_left = make_shared <metal> (color(0.8, 0.8, 0.8),0.3);
auto material_right = make_shared<dielectric>(1.5);
world.add(make_shared<sphere>(point3(0.0, -100.5, -1.0), 100.0, material_ground));
world.add(make_shared<sphere>(point3(-0.5, 0.0, -1.0), 0.5, material_left));
world.add(make_shared<sphere>(point3(0.5, 0.0, -1.0), 0.5, material_right));
|

全内反射
上面的结果是不正确的,如果认真观察斯涅尔定律你会发现,这个公式是有失效的时候的。
光线从较高折射率的介质进入到较低折射率的介质时,如果入射角大于某一临界角θc(光线远离法线)时,折射光线将会消失,所有的入射光线将被反射而不进入低折射率的介质,这种现象叫做全内反射,或称全反射。
拿玻璃举例子,对于光线从玻璃中射入空气的情况,带入

得到:

对于如上的公式,当sinθ大于某特定角度时,sinθ′会大于1,但是sin函数是永远不会大于1的,也就是说,对于这样的角度来说,上述公式会失效。
也就是说,代码得甄别这样的情况,在这种情况下,我们得让光线反射而不是折射。也就是说会有如下的结构:
1
2
3
4
5
6
7
8
9
10
| double cos_theta = dot(-unit_direction, rec.normal);
double sin_theta = sqrt(1.0 - cos_theta*cos_theta);
if (refraction_ratio * sin_theta > 1.0) {
...
} else {
...
}
|
那么只能能折射就折射的代码时是:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class dielectric : public material {
public:
dielectric(double index_of_refraction) : ir(index_of_refraction) {}
virtual bool scatter(
const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
) const override {
attenuation = color(1.0, 1.0, 1.0);
double refraction_ratio = rec.front_face ? (1.0/ir) : ir;
vec3 unit_direction = unit_vector(r_in.direction());
double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);
double sin_theta = sqrt(1.0 - cos_theta*cos_theta);
bool cannot_refract = refraction_ratio * sin_theta > 1.0;
vec3 direction;
if (cannot_refract)
direction = reflect(unit_direction, rec.normal);
else
direction = refract(unit_direction, rec.normal, refraction_ratio);
scattered = ray(rec.p, direction);
return true;
}
public:
double ir;
};
|
施利克近似
一个正确的透明材质会反射部分光线的,入射光线和面的夹角越大,它就越倾向于反射光线。这也就是为什么我们越从掠射角去观察窗户,我们越难看清窗外的景色,而越容易从其上看到自己的脸的原因。
入射光线和法线的夹角和反射率之间的关系是有一个巨大且丑陋的等式所决定的,几乎所有的人都会使用克里斯托弗·施利克(Christophe Schlick)的简单且令人惊讶的精确多项式去近似这个等式。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class dielectric : public material {
public:
dielectric(double index_of_refraction) : ir(index_of_refraction) {}
virtual bool scatter(
const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
) const override {
attenuation = color(1.0, 1.0, 1.0);
double refraction_ratio = rec.front_face ? (1.0/ir) : ir;
vec3 unit_direction = unit_vector(r_in.direction());
double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);
double sin_theta = sqrt(1.0 - cos_theta*cos_theta);
bool cannot_refract = refraction_ratio * sin_theta > 1.0;
vec3 direction;
if (cannot_refract || reflectance(cos_theta, refraction_ratio) > random_double())
direction = reflect(unit_direction, rec.normal);
else
direction = refract(unit_direction, rec.normal, refraction_ratio);
scattered = ray(rec.p, direction);
return true;
}
public:
double ir;
private:
static double reflectance(double cosine, double ref_idx) {
auto r0 = (1-ref_idx) / (1+ref_idx);
r0 = r0*r0;
return r0 + (1-r0)*pow((1 - cosine),5);
}
};
|
施利克近似到底为何物,它到底是如何影响光线选择反射或折射的,先写下它的具体公式:

最终概率落于0到1之间。
公式中只有两个变量:1.两种物质的折射率之比,即 2.夹角的余弦值cosθ。
2.夹角的余弦值cosθ。
它们是怎么影响结果的呢?首先,显而易见的是,θ越小,cosθ越大,反射的概率就越小。也就是说,反射率随着入射光线和法线的夹角增大而增大,这是符合规律的。
其次, 一个容易发现的规律——我们用 去代替公式中的
去代替公式中的 ,最终结果不会有变化,也就是说,对于特定的两种介质,无论哪个是入射光线所在的介质,反射率都遵循一样的规律。
,最终结果不会有变化,也就是说,对于特定的两种介质,无论哪个是入射光线所在的介质,反射率都遵循一样的规律。
还有一个规律,那就是如果 越靠近1,最终解析式中的第二项就越大。即,对于折射率越接近的两种介质,反射概率受θ的影响就越剧烈,反之,θ对于最终反射概率的影响就越小。
越靠近1,最终解析式中的第二项就越大。即,对于折射率越接近的两种介质,反射概率受θ的影响就越剧烈,反之,θ对于最终反射概率的影响就越小。
最后一个规律,对于折射率差距巨大的两种介质, 接近1,第二项接近0,光线极度倾向于反射,罕有折射。
接近1,第二项接近0,光线极度倾向于反射,罕有折射。
在我们的代码中,reflectance(cos_theta, refraction_ratio) 越大,则它越容易大于random_double(),即越容易反射,这是一个经典的利用已知概率和随机数配合进行随机采样的例子。你会得到:

看起来不太像我们见到的玻璃,这是有多种原因决定的:
场景过于简单,在现实世界中,不可能处于这样的场景中,也就不存在对于这种环境下的玻璃材质的视觉直觉。
广角相机,与我们看到的不同,它把远离视角中心的一切物体都拉变形了。
空心玻璃
我们还实现一个空心的玻璃,不需要新的材质,空心玻璃的实现远比你想象的要简单。只需在玻璃球的同样位置放一个稍微小一点的,半径为负值的球即可。半径为负值代表着球的外表面的法线指向球心。通过已经实现的功能,做一个简单的改变就实现了一个玻璃球内“空气泡泡”。
1
2
3
4
5
| world.add(make_shared<sphere>(point3(0.0, -100.5, -1.0), 100.0, material_ground));
world.add(make_shared<sphere>(point3(-0.5, 0.0, -1.0), 0.5, material_left));
world.add(make_shared<sphere>(point3(0.5, 0.0, -1.0), 0.5, material_right));
world.add(make_shared<sphere>(point3(0.5, 0.0, -1.0), -0.4, material_right));
|

拓展
1.空心玻璃球得到的太过简单梦幻,推导实现原理。
推导后发现,负半径使得这句代码vec3 outward_normal = (rec.p - center) / radius;得到的法线是向内的,之后经过rec.set_face_normal(r, outward_normal);函数后因为入射光与法线相反,rec结构体认为光线撞到了物体内部,于是把front_face设置为false,虽然依然得到了向外的法线,但是却为之后的材质判断埋下伏笔。
在材质判断中,是由double refraction_ratio = rec.front_face ? (1.0 / ir) : ir;这句代码判断内外的材质,而front_face为负也导致折射率之比为原来的倒数,则恰好构成由玻璃进入空气的情况。
2.注意到空心玻璃球左侧有一个小黑点,是如何来的呢?
我认为这主要是由于光线打到这个点上由于入射角很大而容易发生镜面反射,所以金属球上,而金属也会反射光线并吸收一部分能量,最后在多次弹射中耗尽了能量而呈现为黑色,可以看到在拉远它们之间的距离后就没有黑点了。

- 事实上,玻璃也不可能完全透明,也就是说,光线碰撞到玻璃材质物体时,会即反射又折射,想想如何实现该材质。
- 了解光栅化中如何实现玻璃材质
参考文献
https://raytracing.github.io/books/RayTracingInOneWeekend.html
参考自《RayTracingInOneWeekend》第10节。
https://en.wikipedia.org/wiki/Refraction
维基百科中对于折射相关的光学知识。
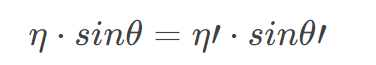


2.夹角的余弦值cosθ。
去代替公式中的
,最终结果不会有变化,也就是说,对于特定的两种介质,无论哪个是入射光线所在的介质,反射率都遵循一样的规律。
越靠近1,最终解析式中的第二项就越大。即,对于折射率越接近的两种介质,反射概率受θ的影响就越剧烈,反之,θ对于最终反射概率的影响就越小。
接近1,第二项接近0,光线极度倾向于反射,罕有折射。


