六：物体列表

实现

有了物体类，我们可以创建单个物体了，但是如果场景物体非常的多，我们则需要一个数组储存它们，不仅如此我们在进行光线的碰撞检测的时候还需要依次调用它们碰撞函数，并且在创景变化或者程序结束的时候去释放内存等等。所以这些操作放在main函数中是不合适的，所以最好的办法是定义一个类去实现这些操作。创建hittable_list.h文件，写入：

#ifndef HITTABLE_LIST_H
#define HITTABLE_LIST_H

#include "hittable.h"

//智能指针的头文件
#include <memory>
#include <vector>

//智能指针！用它来帮我们管理物体列表，就不用担心内存泄漏问题了！
using std::shared_ptr;
using std::make_shared;

class hittable_list : public hittable {
    public:
        hittable_list() {}
    	//当创建物体列表的时候传入了某一个物体，我们直接调用add函数把这个物体加入列表。
    	hittable_list(shared_ptr<hittable> object) { add(object); }

    	//clear函数调用列表的clear函数清空列表。
        void clear() { objects.clear(); }
    	//add函数调用push_back把新物体的智能指针加入列表
        void add(shared_ptr<hittable> object) { objects.push_back(object); }

    	//声明我们需要override父类的hit函数。
        virtual bool hit(
            const ray& r, double t_min, double t_max, hit_record& rec) const override;

    public:
    	//物体列表，使用vector去存每个物体的智能指针。
        std::vector<shared_ptr<hittable>> objects;
};

//重写之后的hit函数。
bool hittable_list::hit(const ray& r, double t_min, double t_max, hit_record& rec) const {
    hit_record temp_rec;
    bool hit_anything = false;
    
    //最开始，把能接受的最远位置设置成外部传进来的t_max。
    auto closest_so_far = t_max;

    //对每个物体做碰撞
    for (const auto& object : objects) {
 		//光线射到了这一堆物体里的某一个。
        if (object->hit(r, t_min, closest_so_far, temp_rec)) {
            //光线有射中东西，把最终函数的返回值设定为true。
            hit_anything = true;
            
            //光线虽然已经射中了一个东西了，但不确定射中的这个物体是不是离相机最近的。
            //范围缩小，然后继续遍历物体列表。
            closest_so_far = temp_rec.t;
            
            //每次有新的碰撞，就设定它的record为最终record。
            //遍历完成后，就可以找到最近的碰撞点并返回它的rec。
            rec = temp_rec;
        }
    }
    //返回这根光线是否有碰到物体列表中的任何物体。
    return hit_anything;
}

#endif

分析

这里面有两个C++非常中要的概念：智能指针和多态

1）智能指针。

C++11给我们提供的瑰宝，它的本质是维护一个指针和一个计数，当创建智能指针并让他指向一个对象的时候，引用计数为1，之后每有一个新的指向它的指针被创建，引用计数加1，一个指针被销毁或者不再指向它，引用计数会下降。引用计数为0则释放对象所占内存。

之前的类我们一直都在“造轮子”，这个物品列表类的作用是管理我们之前做好的“轮子”。通常C++中用于管理一些对象的类，一般都是通过指针去管理。对象之间的传输不仅会占据系统栈的内存，还需要付出因拷贝构造而消耗的时间。

况且通过指针管理对象还有另一层作用，那就是“多态”。

2）多态。

继承结构内的多态的一大实现条件就是基类指针指向子类对象。这是一个极其经典的场景，我们通过虚函数的重写，再通过基类指针定义某一个接口，在实际程序运行过程中无论来的是哪个子类对象，都可以精确的调到对应的虚函数。

在这个程序中，hit函数是如何完成多态的呢？我们的物品列表类只说明了这个列表里面的东西会是一个物体，即它存的是基类指针，hit函数中我们分别调用了列表中每一个指针指向对象的hit函数的，虽然此时并不知道它到底是个球，或者是其他的什么东西，我们只管调用它，多态会帮我们找到具体到底是那个函数并且调用到它。

把物品列表类设计成了物品类的子类还有更多的好处，举一个只有这样设计才能达成的疯狂的玩法！我们可以在这里进行无限层的嵌套！比如下面的某个物品列表：

-物品列表

-子物品列表1

-球1

-球2

-子物品列表2

-球3

-球4

现在给最外层的物品列表调用hit函数，我们问这个列表：“这根光线有没有和这一大堆东西碰撞呀，碰撞结果如何啊？”

最外层的列表说：“我给你看看把，我这里有俩玩意，但我不知道这俩玩意是啥，我帮你找他们问问（最外层列表只知道列表中有俩物体，它不知道这些物体到底是啥）”

紧接着程序开始按照名单给这俩小物品列表发消息：“嘿，你们是什么玩意啊？是球吗？我不管你们是不是球，上面发话了，要看看这根光线有没有和你们碰撞，碰撞情况如何啊？我把光线信息和上面要求的t的范围发给你了啊，再给你一个地址，你们俩把record填好啊！我不管了啊！”

好了，俩小物品列表收到消息也急了，它赶忙找它们下面的东西：“嘿！听的到么！我不管你们是谁，老板要求你们把这根光线…….(省略)”

最外层的物品列表只需要维护自己的closest_so_far，比较两个子物品列表给出的t的大小并选择最小的那个，而再下层的东西它完全不用去管。

这叫什么？递归！我们用“物品列表类是物品类的子类”这一设计，实现了一个精美的递归代码帮我们完成一个光线和一堆物品的碰撞。这也多亏了多态的支持。我无法想象如果我们没有多态，实现一个嵌套列表到底要多出几百倍的代码。

我画了一张类图在来帮助理解这部分代码：

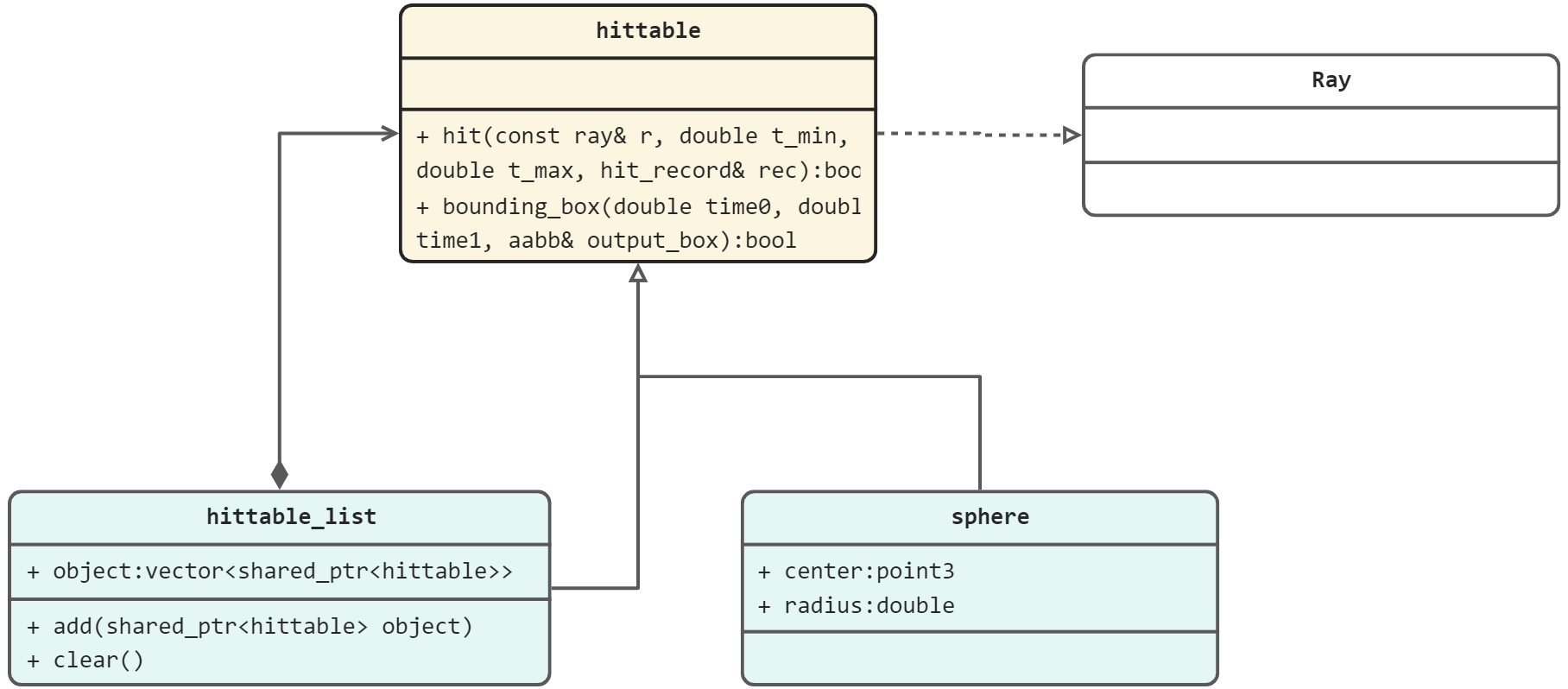
数学类

现在还需要一些常量数字，比如无穷大。不然我们要怎么传最初始的t_max值呢？我们不能在一开始就限定它为10000，1000之类的。显得很不专业，况且，一些常量和一些换算之后还会有更多作用。我们先把我们能想到的写上，之后需要其他的再添加。

文件取名为rtweekend.h，写入：

#ifndef RTWEEKEND_H
#define RTWEEKEND_H

#include <cmath>
#include <limits>
#include <memory>


using std::shared_ptr;
using std::make_shared;
using std::sqrt;

// Constants

// 直接使用C++帮我们定义好的double类型的无限值作为无穷大
const double infinity = std::numeric_limits<double>::infinity();
// Π。 我们先把这个东西放在这，虽然暂时还没有什么用。
const double pi = 3.1415926535897932385;

// 一个角度值转弧度制的函数，嗯。。或许暂时也没有什么用。
inline double degrees_to_radians(double degrees) {
    return degrees * pi / 180.0;
}

//这俩头文件可是我们的常客，之后用他们就直接包这个rtweekend文件就行了。
#include "ray.h"
#include "vec3.h"

#endif

成果

在main函数中写入：

#include "rtweekend.h"

#include "color.h"
#include "hittable_list.h"
#include "sphere.h"

#include <iostream>

//新的光线取色函数中，我们加入了一个名为世界的物体对象，别看它是一个物体对象，我们一般会传入一个物体列表。
color ray_color(const ray& r, const hittable& world) {
    hit_record rec;
    //我们使用到了我们定义的无限大，并且剔除了负t
    if (world.hit(r, 0, infinity, rec)) {
        //没错，依然是元气弹
        return 0.5 * (rec.normal + color(1,1,1));
    }
    //蓝天...
    vec3 unit_direction = unit_vector(r.direction());
    auto t = 0.5*(unit_direction.y() + 1.0);
    return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

int main() {

    const auto aspect_ratio = 16.0 / 9.0;
    const int image_width = 400;
    const int image_height = static_cast<int>(image_width / aspect_ratio);

    // 创造世界
    hittable_list world;
    
    //插入俩个球
    //和以前一样
    world.add(make_shared<sphere>(point3(0,0,-1), 0.5));
    //一个非常吓人的巨型球！
    world.add(make_shared<sphere>(point3(0,-100.5,-1), 100));

    //摄像机相关
    auto viewport_height = 2.0;
    auto viewport_width = aspect_ratio * viewport_height;
    auto focal_length = 1.0;

    auto origin = point3(0, 0, 0);
    auto horizontal = vec3(viewport_width, 0, 0);
    auto vertical = vec3(0, viewport_height, 0);
    auto lower_left_corner = origin - horizontal/2 - vertical/2 - vec3(0, 0, focal_length);

    //渲染循环（render loop）
    std::cout << "P3\n" << image_width << ' ' << image_height << "\n255\n";

    for (int j = image_height-1; j >= 0; --j) {
        std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
        for (int i = 0; i < image_width; ++i) {
            auto u = double(i) / (image_width-1);
            auto v = double(j) / (image_height-1);
            ray r(origin, lower_left_corner + u*horizontal + v*vertical);
            //和原来没什么不同，也说明了作者的封装非常完美
            color pixel_color = ray_color(r, world);
            write_color(std::cout, pixel_color);
        }
    }
    std::cerr << "\nDone.\n";
}

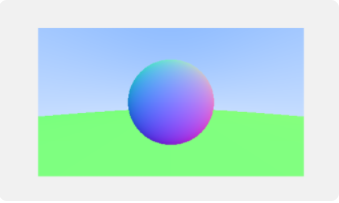
于是我们得到了在一片草原之上的元气弹，实际上只是球体所在位置及其表面法线的可视化。这通常是查看模型缺陷和特征的好方法。

参考文献

https://raytracing.github.io/books/RayTracingInOneWeekend.html

参考自《RayTracingInOneWeekend》第6.5节到第6.7节。