祥瑞客栈

记录点滴的成长

0%

四：球

发表于 更新于 分类于 Valine：

基础概念

接下来总要让一个对象让光线碰撞，这里选择使用最简单的物体：球

一个非常标准的球的数学表达式，这个公式表示以原点为球心，半径是R的球。所有坐标是（x,y,z）的点满足上面的表达式都在球上。接下来是点在球内和求外的公式：

假定球心为$(C_x,C_y,C_z)$

但是这个公式没有办法在我们的项目中使用，我们的底层使用的vec3类，更希望看到向量而不是标量表示，我们需要简单的改变一下这个公式。现在假设球形所在的坐标用C这个vec3类常量表示，即$C=(C_x,C_y,C_z)$。同样的令$P=(x,y,z)$有：

上述式子的左侧是一个向量模的平方，右侧是一个距离公式。它们都表示P点和C点之间的距离的平方。所以有：

所有满足这样要求的P——它到C点的距离为r，这样的点一定在以C为球心，r为半径的球上。

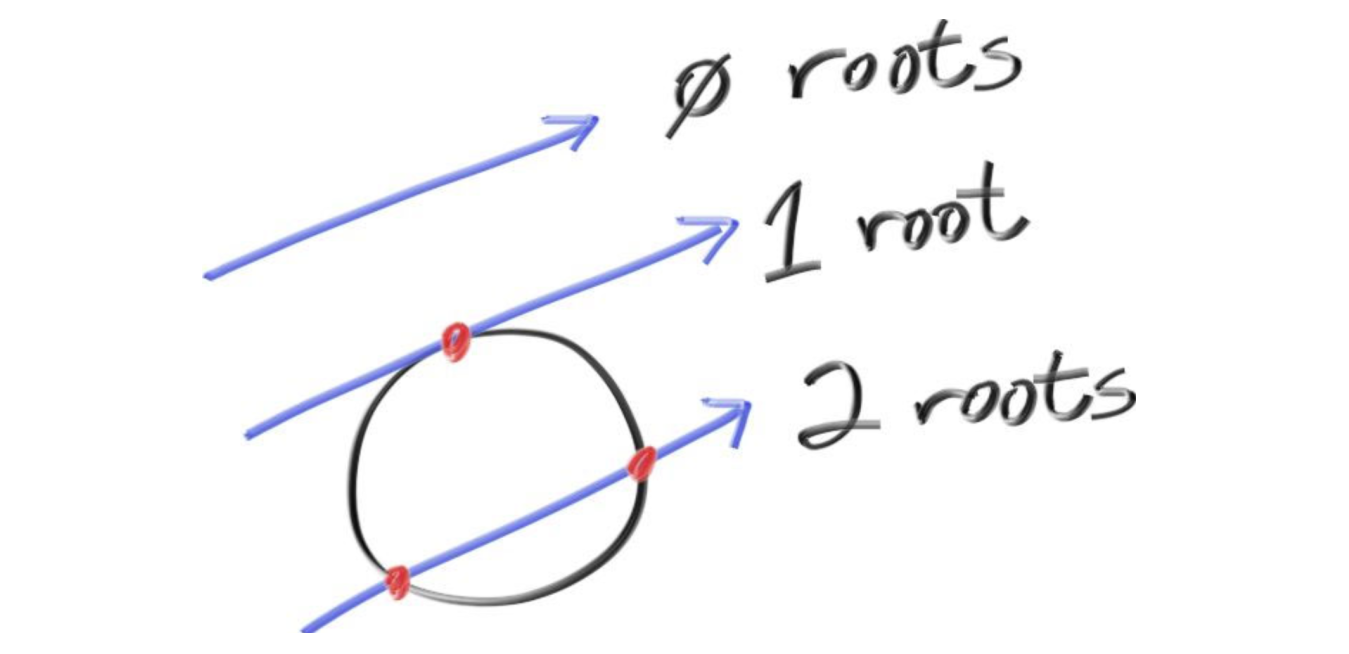
现在引入光线，如果光线曾在某一个时刻打在球上，则表示有一个t，使得$P(t)=A+tb$正好传播到了球的位置。带入它之后：

展开：

把左侧括号乘开，这里我们把$(A-C)$看作一个整体，再把右侧的移$r^2$到左侧。

变成了一个t的一元二次方程。（b表示光线方向，A是光源位置，C是球心，全是常量）。

碰撞函数

在.cpp文件中main函数外写入：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//简易的球的碰撞检测函数，吃球心，半径和一根光线，吐出光线是否击中球的bool值。
bool hit_sphere(const point3& center, double radius, const ray& r) {
    // 这个oc就是上面函数里的(A-C).
    vec3 oc = r.origin() - center;
	// 对应上面公式里的b的平方。即平方项的系数。
    auto a = dot(r.direction(), r.direction());
    // 对应上面公式里的2*(A-C)点乘b，即一次项的系数
    auto b = 2.0 * dot(oc, r.direction());
    // (A-C)点乘(A-C)减去r的平方，即常数项。
    auto c = dot(oc, oc) - radius*radius;
    //高中最爱的Δ，b的平方减4ac。
    auto discriminant = b*b - 4*a*c;
    //返回方程有没有根，即光线有没有碰撞到球体。
    return (discriminant > 0);
}

color ray_color(const ray& r) {
    // 如果我们击中了这个球心在(0,0,1)且半径是0.5的球，就直接返回颜色为红色。
    if (hit_sphere(point3(0,0,-1), 0.5, r))
        return color(1, 0, 0);
    // 如果没有击中的话你就继续画蓝天吧。
    vec3 unit_direction = unit_vector(r.direction());
    auto t = 0.5*(unit_direction.y() + 1.0);
    return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

最终得到了一个不那么美丽的太阳！

image-20220306223618931

可视化法线

如果我们得知光线和球的碰撞点为P，我们需要得到这一点的法线，它应该是从球心发射，穿过这一点指向球的外侧，所以是img。

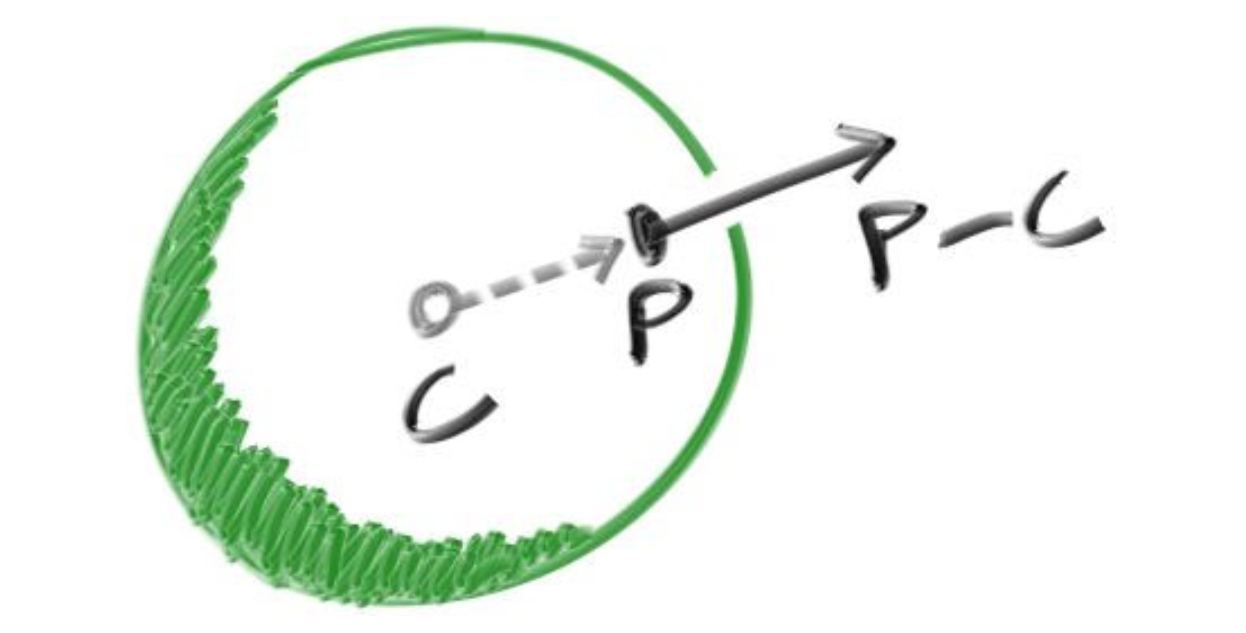
image-20220306223737173

这里需要考虑两个问题：

  • 它应该是单位向量吗？是的，它应该是，单位化法线可能会在某些方面为我们的渲染提供便利，但是不强制，并不要求法线一定是单位向量，如果必须是单位化的地方我们进行单位化即可。为了省去这一步骤这里选择永远单位化它。
  • 之前我们给的hit_sphere函数的框架已经不足以满足我们获取法线的需要了，因为这里不仅仅需要了解球和光线是否碰撞，我们还得知道光线和球的第一个焦点的位置，因为只要不是极端的相切的情况，我们总能找到两个焦点，所以我们需要t较小的那个焦点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
//它不再返回bool，而是返回一个浮点数，表示光线第一次打在球上的时候的时间t。
double hit_sphere(const point3& center, double radius, const ray& r) {
    vec3 oc = r.origin() - center;
    auto a = dot(r.direction(), r.direction());
    auto b = 2.0 * dot(oc, r.direction());
    auto c = dot(oc, oc) - radius*radius;
    auto discriminant = b*b - 4*a*c;
    if (discriminant < 0) {
        // Δ小于0，别看了，光线没打到球，直接返回一个负值。
        return -1.0;
    } else {
        // 求根公式，我们返回了较小的那个根。
        return (-b - sqrt(discriminant) ) / (2.0*a);
    }
}

//通过得到的法线返回颜色
color ray_color(const ray& r) {
    auto t = hit_sphere(point3(0,0,-1), 0.5, r);
   
    //如果光线击中了球。
    if (t > 0.0) {
    	//拿到法线，嘿嘿，我们之前写过很久的at函数终于派上用场了。我们这次单位化它。
        vec3 N = unit_vector(r.at(t) - vec3(0,0,-1));
        //返回法线可视化之后的颜色值，注意我们做了一个[-1,1]到[0,1]的映射。
        return 0.5*color(N.x()+1, N.y()+1, N.z()+1);
    }
    
    //如果没打中？继续画蓝天吧。
    vec3 unit_direction = unit_vector(r.direction());
    t = 0.5*(unit_direction.y() + 1.0);
    return (1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);
}

这里将hit_shpere函数的返回值由bool改为第一次碰撞的时间t，并在取色函数中通过时间t获取碰撞点，并计算出法线，最后将法线映射为颜色，最终我们可以看到一个元气弹！

image-20220307085406164

拓展问题

  1. 在红太阳阶段的代码中如果将太阳放在相机后面会发生什么呢？
1
2
if (hit_sphere(point3(0,0,1), 0.5, r))
        return color(1, 0, 0);

image-20220306223618931

可以看到与放在相机前没有任何变化，我认为是主要是因为这段代码虽然判断了碰撞函数是否有解，但是忽略了t小于0 的情况，以至于放在相机前后没有区别，用第二段代码就没有任何问题。

  1. 元气弹的颜色遵循什么规律呢？

按照代码逻辑应该是碰撞法线x,y,z分量分别对应r,g,b的值。那么应该是向右越来越红，向上越来越绿，由中心向外越来越蓝。

  1. 使用元气弹版本的代码，更改hit_sphere函数，这次返回较大的那个根，生成图片另外保存。
1
2
// 求根公式，这次返回较大的那个根。
return (-b + sqrt(discriminant)) / (2.0 * a);

image-20220307092334496

参考文献

https://raytracing.github.io/books/RayTracingInOneWeekend.html

参考自《RayTracingInOneWeekend》第5节和第6.1节。